线性规划对偶

一直都想学的引荐东西了。

瞎给个 link。

不会证明，所以直接贴个结论。

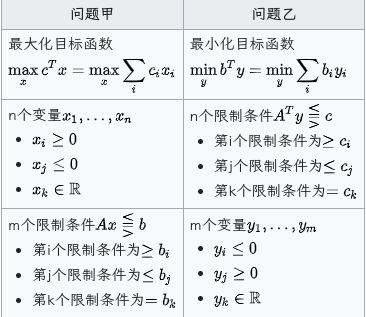
再贴个例子：

主要可以用来解决操作种类很多，但是约束比较少的线性规划题，这样可以把约束和变量数交换，简化问题。

loj3313

Bob 喜欢序列。

有一个长度为 $n$ 的非负整数序列 $a_1, a_2, \dots, a_n$。每一步你可以从以下三种操作中选择一种执行：

• 选择一个区间 $[l, r]$，将下标在这个区间里的所有数都减 $1$。

• 选择一个区间 $[l, r]$，将下标在这个区间里且下标为奇数的所有数都减 $1$。

• 选择一个区间 $[l, r]$，将下标在这个区间里且下标为偶数的所有数都减 $1$。

求最少需要多少步才能将序列中的所有数都变成 $0$。

$n\le 10^5$

经典题了，虽然贪心做法一车，但作为线性规划入门还是不错的。

直接假设三种区间操作个数为 $x_{l,r},y_{l,r},z_{l,r}$。

写出标准形式：

$$\min \sum_{1\le l\le r\le n} x_{l,r}+y_{l,r}+z_{l,r}\\ \begin{cases} \sum_{i\in [l,r]} x_{l,r}+y_{l,r}=a_i & {n\bmod 2=1} \\ \sum_{i\in [l,r]} x_{l,r}+z_{l,r}=a_i & {n\bmod 2=0} \end{cases} \\ \forall x_{l,r},y_{l,r},z_{l,r}\ge 0$$

直接对偶：

$$\max \sum a_ik_i\\ \forall l,r\\ \sum_{i=l}^r k_i\le 1 \\ \sum_{i=l}^r [i\bmod 2=1]k_i\le 1\\ \sum_{i=l}^r [i\bmod 2=0]k_i\le 1\\ k_i\in \mathbb{R}$$

容易发现 $k_i\in [-1,1]$。

证明 $k_i$ 是整数其实是困难的，但一般做题时是大胆猜测。

于是一个简单 dp 即可，记录一下前面的最大值。